1. Blackjack Bankroll Risk Of Ruin Death
2. Blackjack Bankroll Risk Of Ruin The Following
3. Risk Of Ruin Blackjack Calculator

• Appendices
• Miscellaneous
• External Links

$1,000 Bankroll – $10/hr EV; 45% Risk of Ruin. Now that seems like lot of risk, but you also have a 55% chance of never looking back and doubling your bankroll in 100 hours. Does this mean you need $1,000 before you start playing? That's the point of having a money management system for blackjack. Blackwood suggests that you lower your bet size only if you lose 20% of your bankroll - again, I would follow his system. Lowering Your Risk at Blackjack. A simple way to lower your risk is to play in more profitable games or to use more profitable systems for counting cards.

Introduction

There are some sources that address the question of the probability of doubling a bankroll before losing it, in a card counting situation. Ken Uston's Million Dollar Blackjack, to name one. This appendix shall not recover that issue. However, I am often asked about how much the basic strategy player's bankroll should be, given a targeted number of hands to play. This is especially practical if the player must play a certain number of hands to earn an online casino bonus.

The rules assumed for these tables are six decks, dealer stands on soft 17, player may double on any two cards, player may double after splitting, player may resplit to three hands, no surrender, dealer peeks for blackjack. Under these rules, the house edge is 0.4140%.

Let's look at an example of how this table can be used. Assume that the player makes a deposit of $1000 to an online casino, and is required to bet through $5000 in action. If the player is to willing to play through 500 hands, then his average bet size would be $5000/500 = $10. The number of betting units would be $1000/$10 = 100. The table shows the risk of ruin is 0.01% for 102 units, so would be just over 0.01% for 100. Perhaps this is too conservative, so the player considers playing 200 hands. The bet size is now $5000/200 = $25. The number of units is $1000/$25 = 40. Interpolating the table shows the risk of ruin would be 1.5%.

Number of Hands to Play

Risk of Ruin	100	200	300	400	500	600	700	800	900
50%	7	11	14	16	18	20	22	24	25
40%	9	14	17	20	23	25	27	29	31
30%	12	17	21	25	28	31	33	36	38
20%	15	21	26	31	34	38	41	44	47
10%	19	27	34	39	44	48	53	57	60
5%	22	32	40	46	52	58	62	67	71
4%	23	34	42	49	55	60	65	70	75
3%	25	36	44	51	58	64	69	74	79
2%	27	38	47	55	62	68	74	79	84
1%	29	42	52	61	68	75	82	88	93
0.5%	32	46	57	66	74	82	89	95	101
0.25%	35	50	61	71	80	88	96	102	109
0.1%	38	54	67	77	87	95	104	111	118
0.01%	45	64	79	91	102	112	122	131	139

Blackjack Bankroll Risk Of Ruin Death

Number of Hands to Play

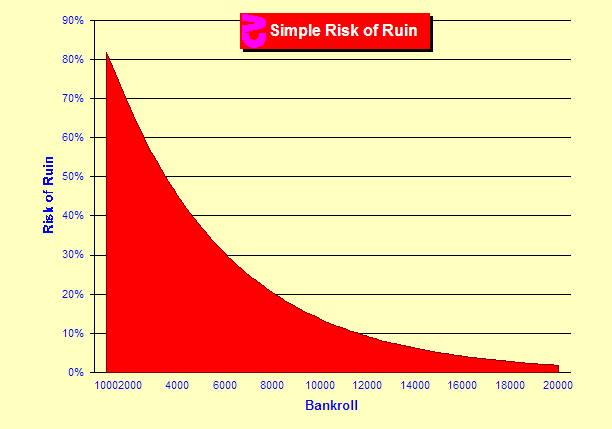
Risk: Risk given no goal and no time constraint - This is the Simple Risk of Ruin formula on Blackjack Attack page 112. The result is the risk of ruin with no limit on the number of hands and no quit point. Simply set the bankroll. Risk given no goal but a time constraint - This is the trip ruin formula in Blackjack Attack page 132. Of course, the table also shows you how much risk is associated with playing blackjack with a given bankroll. In order to keep the risk of ruin under 0.5%, a bankroll of 1700 units is required. This, in turn, is enough to make 1.57 units/hour.

Blackjack Bankroll Risk Of Ruin The Following

Risk of Ruin	1000	1200	1400	1600	1800	2000	2500	3000
50%	27	30	32	35	37	40	45	50
40%	33	37	40	43	46	49	56	62
30%	41	45	49	53	56	60	68	75
20%	50	55	60	65	69	73	83	92
10%	64	70	76	82	88	93	105	116
5%	76	83	90	97	104	110	124	137
4%	79	87	95	102	108	114	129	143
3%	83	92	100	107	114	121	136	151
2%	89	98	107	114	122	129	145	161
1%	99	108	118	126	134	142	160	177
0.5%	107	118	128	137	146	154	174	192
0.25%	115	126	137	147	156	166	187	206
0.1%	125	138	149	160	170	180	202	223
0.01%	148	162	175	188	198	212	236	261

Methodology

The tables above were created by random simulation. I have been asked several times for a general formula for other situations. Unfortunately there isn't any that I know of. Risk of ruin problems are mathematically usually very complicated. It is easier and more convincing to run a random simulation instead.

Risk Of Ruin Blackjack Calculator

Written by: Michael Shackleford